
Hi folks!
Growing Meta is a hub for the most insightful bites of scholarly conclusions and discoveries that augment our understanding of knowledge & complexities. Share it with people who want to hop on this hot air balloon ride!
My week in points:
[Essay] Study Debates to Accelerate your Learning Journey. What is the fastest way to learn a new field? You can take a 4-year degree, hire consultants, or read a few textbooks, but knowing the issues that set experts apart will give you the highest degree of exposure (to important ideas and people in that field) quickly.
[Thread] My lessons learned from doing a 2-year long thesis project. I graduated from the University of Melbourne’s master program for computer science last year, with some challenges. I was pregnant and gave birth in the last semester. I actually wrote the majority of my thesis when I was nursing Rawwaf (who’s now 1.5 years old!) Here are a few lessons that any post-grad student can learn the easy way:
Fractals: “Never Ending Patterns”
I was reading again on fractals this week, such a fascinating weird phenomenon.
Fractals are objects with ’self-similarity’ at different scales.
Mandelbrot, a mathematician, first gave a name to this phenomena when he was trying to develop a theory of ‘roughness’ in the world. That meant that he was trying to explain how the natural world is designed.
Look at trees, stock markets, mountain ranges, space, the World Wide Web, cauliflower, and language.
They all have the same pattern if you zoom in, or if you zoom out.
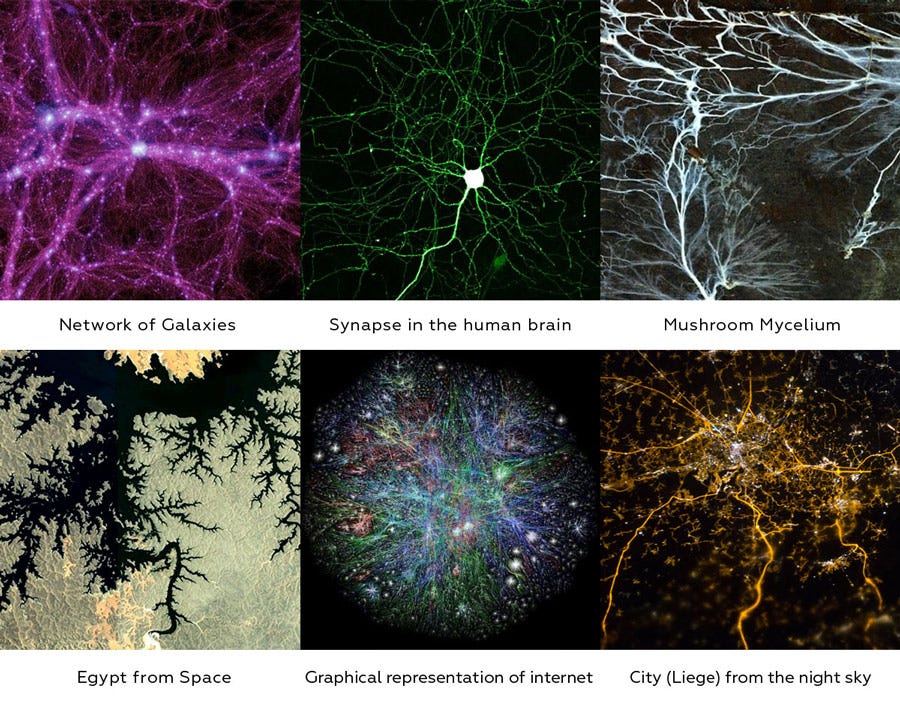

(Images source: Void Visuals)

(Image source: Scaling in the Norwegian stock market.[1])
[Fractals] can be used to solve a variety of problems including predicting weather, designing antennae, and even characterizing metals. [2]
Tim Berners Lee (who invented the WWW) explores the fractal nature of the semantic web [2] — the part of the WWW whose goal is to make machines understand data through standards. Tim writes that we should look at patterns of usage (because at any scale - individual or organizational - users perceive data internally the same way), rather than at technical aspects when designing standards.
The Coastline Paradox
An uncomfortable observation was made [3]: The length of your country’s coastline depends on your ruler’s length. If your shore is a straight line, it’s an easy measure (from A to B). But it’s not a straight line, it’s a fractal.

(GIF source: Cartographers without Borders)
Length of the coastline of Great Britain can vary between 17.7k and 5.3k kilometers (11k and 3.3k miles), depends on how small your ruler is.
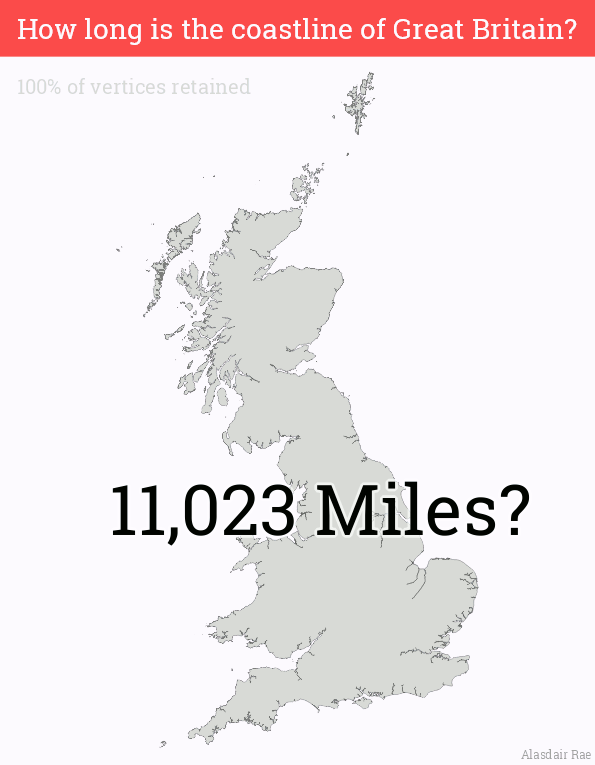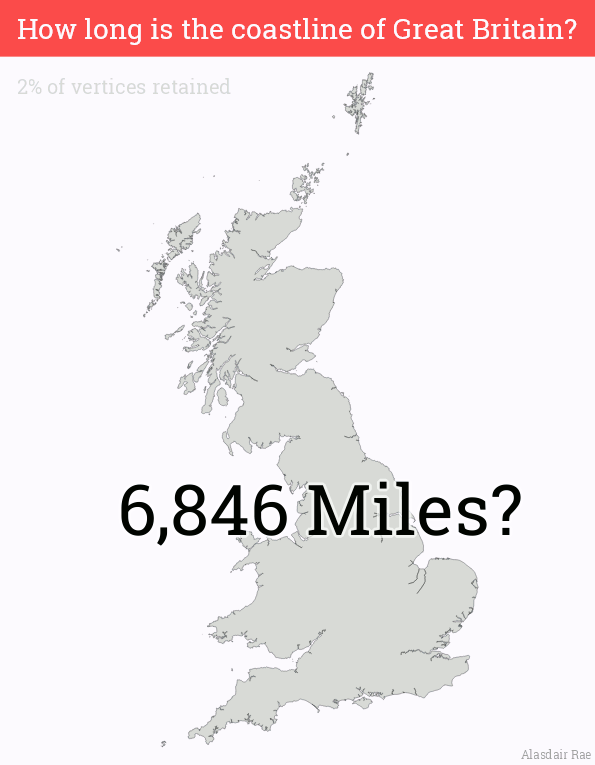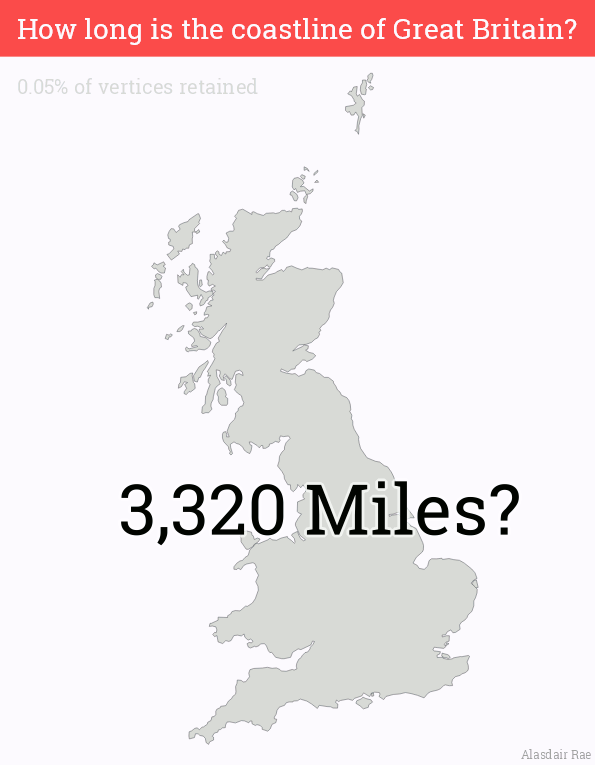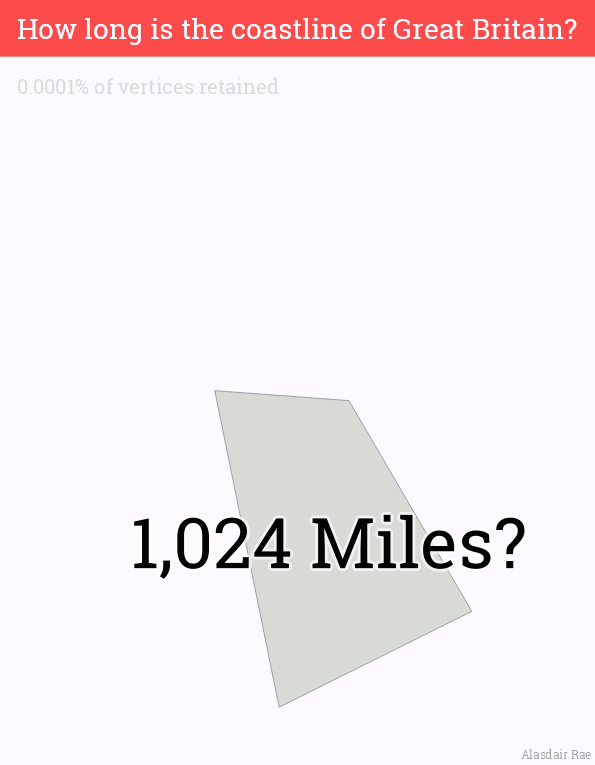
(GIF source: Alasdair Rae)
So how do we measure the length of a coastline, or any fractal?
It’s weird, but fractals are not 1D, 2D nor 3D. They are not easily measurable. Mandelbrot conceptualized the ‘fractal dimension’ to solve this gap (here’s a video to explain it.), there are different ways to calculate it.
For example, a cauliflower’s fractal dimension is not 3D, it’s 2.8D!

(GIF source)
Meta Finds
[Article] Fractal Patterns Offer Clues to the Universe’s Origin - Wired
[Book] The (Mis)Behaviour of Markets: A Fractal View of Risk, Ruin and Reward.
Benoit B. Mandelbrot and Richard L. Hudson write this book to illustrate how fractals apply to financial markets. I haven’t read it, but getAbstract “thinks every investor, every business journalist and every financial professional ought to read this book.” They gave it a 10/10.
Mandelbrot also has a lot of papers on financial markets with Nassim Taleb.
[Gaming Engine] Fractal Physics Engine. There is always a tradeoff between accuracy and speed of collision physics in game engines. This developer proposes collapsing objects into fractals when calculating collision and response angles. He then gracefully created a beautiful game Marble March, which is built on his engine.
[Game] Fractal Drawing Game. Fun web app where you can draw fractals.
Reply to This
Mandelbrot looked at mountains, stock markets, coastlines, cauliflowers, snails (amongst other things) and saw self-similarity at different scales. He called it fractals.
Is there one thing that you see in many different things?
Share it with me and I’ll look in the literature and see if someone has found a name for it (if I can’t find it, you can give it a name and call yourself an observational scientist!)
[1] Ikeda, Taro. "A fractal analysis of world stock markets." Economics Bulletin 37.3 (2017): 1514-1532.
[2] Berners-Lee, Tim, and Lalana Kagal. "The fractal nature of the semantic web." AI magazine 29.3 (2008): 29-29.
[3] Weisstein, Eric W. "Coastline Paradox." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/CoastlineParadox.html




